Güvercin Yuvası Prensibi

Güvercin Yuvası Prensibi

Genellikle Güvercin Yuvası Prensibi olarak bilinen bu ilke aynı zamanda “Çekmece İlkesi”  veya “Dirichlet Kutu (çekmece) ilkesi” olarak da bilinmektedir.

İngilizce kullanımı ise “Pigeonhole Principle (Güvercin Prensibi)” şeklindedir.

Ünlü matematikçi Gauss’a dayandırılan bir hikayeyle anlatılan ünlü matematiksel ilke.

Çok basit bir ilke olmasına rağmen bu ilkeyi kullanarak ispatlanabilecek ilişkiler çok ilginç olabilir.

Gauss’a dayandırılan bir hikaye şu şekildedir;

Küçük Gauss babasıyla ormanda gezerken sormuş:
− Bu ormanda yaprak sayısı aynı olan iki ağacın olması için herhangi bir koşul söyleyebilir misin? Baba Gauss böyle bir koşul düşünemeyince yanıtı küçük Gauss vermiş:

− Eğer ormandaki yapraklı ağaç sayısı, bu ormanın en çok yaprağı olan ağacın yaprak sayısından daha fazlaysa, en az iki ağacın yaprak sayısı aynıdır.

Bu hikaye her ne kadar uydurma gibi görünse de en azından Gauss’un çok ünlü bir matematikçi olması durumu bir nebze de olsa kurtarıyor.

Bu ilke tam olarak şunu der: N ve k pozitif tamsayılar ve N > k olmak üzere N nesne k kutuya yerleştirildiğinde öyle bir kutu vardır ki o kutuda birden çok nesne bulunmak zorundadır. Bu doğru olmasaydı, yani her kutuda en fazla birer nesne olsaydı, k kutuda en fazla k nesne olabilecekti.

Matematikte, Güvercin Yuvası Prensibi, öğelerin kaplara konulması durumunda, en az bir kabın birden fazla öğe içermesi gerektiğini ifade eder.

Şimdi daha anlaşılabilir bir örnek verelim. Ülkemizde yaygın bir şey olan güvercin besleme olayını bir an için kendinizin de yaptığınızı düşünün ve güvercinleriniz akşam olduğu için yuvalarına girmeye hazırlanmakta olduğunu var sayalım.

Eğer güvercin sayısı güvercin yuvası sayısından fazlaysa, örneğin 9 yuva ve 10 güvercin varsa, en az bir yuvada birden fazla güvercin olmak zorundadır. İşte bu ilkeye Güvercin Yuvası Prensibi isminin verilmesinin sebebi de bu açıklamadır.

Farklı bir örnek daha verilebilir:

Bir torbada 30 mavi 30 kırmızı toplam 60 topun olduğunu düşünelim. Hangi renk olduğuna bakmadan rastgele birini seçelim.

En az kaç top seçmeliyiz ki seçilenlerden en az biri kırmızı olsun?

Seçeceğimiz topların birisinin kesinlikle kırmızı olmasını istediğimize göre en kötü ihtimali düşünüp 30 seçimin 30’unun da mavi top olduğunu düşünelim. Böylece 31. seçimde seçeceğimiz top kesinlikle kırmızı olacaktır.

Güvercin Yuvası Prensibinin Genelleştirilmesi

Bu prensibin genelleştirilmiş hali; eğer n ayrık obje m kaba yerleştirilecekse en az bir kap ‘den az olmayacak şekilde obje barındırır şeklindedir, [x] tavan fonksiyonudur (en: ceiling function), x’den büyük x’e en yakın veya x’in kendisi olan tam sayıya eşitler.

Olasılıksal genelleştirilmesi; eğer n güvercin rastgele m adet güvercin deliğine 1/m olasılıkla koyulursa en az bir güvercin deliği

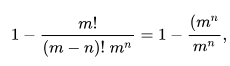
olasılıkla birden fazla güvercin tutacaktır, (m)_n, permutasyon(en:Falling Factorial)’dur. n = 0 ve n = 1 (ve m > 0) için, olasılık sıfırdır, başka bir deyişle, eğer tek bir güvercin varsa bir çekişme olmayacaktır.

n > m (güvercin deliklerinden daha çok güvercin) olduğunda çekişme olur, bu durumda bilinen güvercin deliği prensibi ile uyuşur. Ama güvercin sayıları güvercin deliği sayısını aşmazsa (n ≤ m)güvercinleri güvercin deliklerine rastgele yerleştirmenin doğasından genelde bir çakışma meydana gelir.

Örneğin, eğer iki güvercin rastgele 4 güvercin deliğine yerleştirilirse, 25% ihtimalle bir güvercin deliği birden fazla güvercin tutar; 5 güvercin ve 10 delik için olasılık 69.76% olur; ve 10 güvercin ve 20 delik için yaklaşık 93.45% olur. Bu problem doğumgünü paradoksu(en: Birthday Paradox)‘nda daha büyük bir uzunlukta olur.

Kaynaklar:

1. Herstein 1964, p. 90
2. Jeff Miller, Peter Flor, Gunnar Berg, and Julio González Cabillón. “Pigeonhole principle”. In Jeff Miller (ed.) Earliest Known Uses of Some of the Words of Mathematics. Electronic document, retrieved November 11, 2006
3. Fletcher & Patty 1987, p. 27
4. Diskrete Mathematik – Page 367 https://books.google.at/books?isbn=3833455292
5. The Induction Book – Page 13 https://books.google.at/books?isbn=0486811999
6. Mathematics Dictionary – Page 490 https://books.google.at/books?isbn=0412990415
7. To avoid a slightly messier presentation we assume that “people” in this example only refers to people who are not bald.
8. <https://books.google.com/books?id=GG0PAAAAQAAJ&q=town+eternity>
9. Rittaud, Benoit; Heeffer, Albrecht (2014), “The Pigeonhole Principle, Two Centuries before Dirichlet” (PDF), Mathematical Intelligencer, 36 (2): 27–29, doi:10.1007/s00283-013-9389-1
10. Leurechon, Jean (1622), Selecæe Propositiones in Tota Sparsim Mathematica Pulcherrimæ, Gasparem Bernardum, p. 2
11. Grimaldi 1994, p. 277
12. Introduction to Formal Languages and Automata, Peter Linz, pp. 115–116, Jones and Bartlett Learning, 2006
13. Computational Geometry in C, Cambridge Tracts in Theoretical Computer Science, 2nd Edition, Joseph O’Rourke, page 9.
14. Brualdi 2010, p. 74 Theorem 3.2.1
15. In the lead section this was presented with the substitutions m = n and k = r − 1.